Distribuţia bogăţiei - I

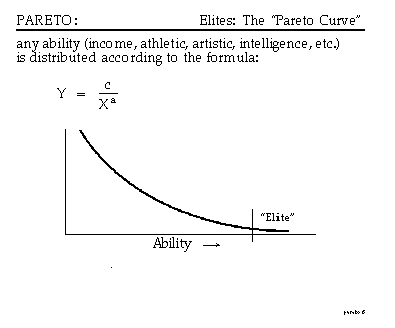
Să vorbim întâi despre legea lui Pareto. Până la descoperirea acestei legi pe care o să o explic în continuare se credea că distribuţia bogăţiei în societate depinde de condiţiile economice ale unei ţări, de resurse, de nivel de educaţie al populaţiei, de structura sectorială a economiei etc.

Legea lui Pareto, greşit numită legea 80 - 20, ne spune, pe scurt, că distribuţia bogăţiei în societate se face după o formulă, N=x/(B^y) . N este numărul de cetăţeni care posedă cantitatea B, x parametru pozitiv, y este un parametru pozitiv mai mare ca 1. Cu cât este mai mare cantitatea de bunuri B cu atât avem mai puţini cetăţeni care posedă această cantitate. Banii sunt practic în mâna unei minorităţi restrânse.


Până în anul 2000 nu exista o explicaţie pentru această lege. Parametrii sunt diferiţi de la ţară la ţară dar legea funcţionează peste tot. Jean-Philippe Bouchaud şi Marc M´ezard (lucrarea e sinistră pentru majoritatea covârşitoare, inclusiv pentru mine), doi fizicieni specializaţi în fizica materialelor, au început să dezvolte un model economic de la zero. Au presupus, spre nedumerirea majorităţii economiştilor care postulează comportamentul perfect raţional al agenţilor economici, că viaţa e impredictibilă. Că investiţiile sunt impredictibile ca valoare în timp, căderi sau salturi spectaculoase la bursă sau case la preţuri astronomice care se prăbuşesc, preţurile nu casele, toate acestea le trăim. Mai mult, tunuri sau ţepe economice există peste tot, sunt greu de pus într-un model. Aşa că e mai simplu să considerăm lucrurile impredictibile. Imaginea este de aici.

Au mai presupus că fiecare agent economic face comerţ cu alţi câţiva aleşi la întâmplare, în realitate nu e chiar aşa dar vedem mai târziu. O altă presupunere, venită din fizică, este invarianţa modelului la moneda folosită, nu contează ce monedă e folosită în tranzacţiile dintre agenţi. Şi au mai făcut o presupunere de bun simţ, că oamenii bogaţi investesc mai mult decât cei săraci, deci câştigă sau pierd mai mult, am presupus că viaţa e impredictibilă.

Deci toţi agenţii economici formează o reţea, fac tranzacţii între ei, investesc relativ proporţional cu averea pe care o au, rezultatul investiţiilor este impredictibil. După o vreme distribuţia bogăţiei urmează curba lui Pareto cu o valoare a parametrului y între 2 şi 3. Chiar dacă la început toţi aveau aceeaşi sumă şi oricum este reţeaua formată curba lui Pareto de distribuţie a bogăţiei pare sau chiar este un dat al naturii economiei.

Aşa că, în acest prim episod, următorul mâine, putem concluziona. Eradicarea diferenţelor sociale e imposibilă, înlăturarea actualilor bogaţi o să aducă alţii în faţă. Socialismul este o utopie, o să vedem că atunci de fapt toţi sunt săraci şi extrem de puţini bogaţi. Dar nu orice curbă a lui Pareto este la fel de nedreaptă şi există factori care pot conduce la o distribuţie mai echitabilă a bogăţiei, un y mai mic. De asemenea distribuţia bogăţiei nu e la fel de la ţară la ţară în sensul că acelaşi loc pe scală în 2 ţări diferite nu înseamnă aceeaşi bogăţie, o ţară poate să fie în ansamblu mai bogată (x1>x2).

Ca o ultimă concluzie pentru prima parte este că nu discutăm despre indivizi ci despre o ţară în ansamblul ei sau despre întreaga lume. Nu vă lansaţi în concluzii definitive că povestea e mai lungă.

Mulţumesc anonimului care mi-a semnalat articolele. Domeniul din care face parte o asemenea lucrare se cheamă economie computaţională.

PS Regulile comentariilor sunt aici, încălcarea lor se pedepseşte cu ştergerea fără avertisment.